Fishers Ideal Index Number: Calculation, Features and Limitation

TORAN LAL VERMA

Fishers Ideal Index Number is one the important price index number. Prof Irving Fisher developed this index number after an extensive study of 134 different formulae. It is a type of weighted index number.

Calculation Process: Calculation process of fishers formula is as follows

  1. For calculation, 9 columns are drawn. First columns for commodities, second for price in base year (P0), third for quantity in base year (q0), Fourth for price in current year (p1) and fifth for quantity in current year (q1). In remaining four columns different prices and quantities are multiplied as per the requirement of the formula.
  2.  ∑p0q0   is obtained by totaling the multiplication of price p0 and q0 and quantity(q0) of each commodity is base year.
  3. ∑p1q0   obtained by totaling the multiplication of price in current year p0 and quantity in base year (q0) in respect of each commodity.
  4. ∑p0q1   obtained by totaling the multiplication of price in base year (p0) and quantity in current year (q1) in respect of each commodity.
  5. ∑p1q1    is obtained by adding the products (p1) and quantity (q1) of each commodity in current year.
  6. Finally, the following formula is used

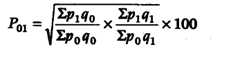
Features of Fisher’s Ideal Index Number

  1. Use of Variable Weights: In this formula variable weights are used i.e. different weights are used in base year and current year on the basis of quantities in these years. it is practival also becauise quantity of consumption may not remain the same every year.
  2. Based on Geometric Mean: Fisher’s index is based on geometric mean which is supposed to be the best average for the construction of index numbers. This index number is also called geometric mean of the Laspeyre’s and Paashe’s index numbers.
  3. Satisfaction of Reversal Tests: It satisfies the time-reversal as well as the factor reversal tests.

Limitations of Fisher’s Ideal Index Number

Though Fisher’s formula is an ideal formula of an index number, yet it has the limitation that the data of the quantity of each year also should be available, otherwise this index number cannot be calculated. Moreover, this index number does not indicate the change in price only but it gives information about the mixed change in price and quantity.

Boddington has remarked that “Unfortunately, while this formula apparently meets most of the mathematical requirements of a perfect index formula, it is objected to on the score that it is not clear what it measures, i.e., the result combines both price and volume changes, when usually we want the one to be separated from the other.”

This content is taken from the book Statistical Analysis by SM Shukla and KL Gupta click here to buy the book

link

Share with friends